Soutien Scolaire Gratuit !!!
- Dr.Snap
- Membre
- Messages : 6041
- Enregistré le : lun. 30 avr. 2007, 01:24
- Localisation : Etage 442 Tour Sacrée Hospital Section TLP
- Contact :
Re: Soutien Scolaire Gratuit !!!
Polynôme du second degré : ax² + bx + c
Dérivée : 2ax + b
En fait, la dérivée de x^n est nx^(n-1)
Par exemple, la dérivée de x² est 2x, la dérivée de x^3 est 3x², ....
Et on garde les coefficients devant : la dérivée de 4x² est 8x.
Dérivée : 2ax + b
En fait, la dérivée de x^n est nx^(n-1)
Par exemple, la dérivée de x² est 2x, la dérivée de x^3 est 3x², ....
Et on garde les coefficients devant : la dérivée de 4x² est 8x.
 -
-  -
- 

- Saer Myenn
- Membre
- Messages : 4020
- Enregistré le : mer. 27 janv. 2010, 21:43
- Localisation : Tout est bon chez le héron
Re: Soutien Scolaire Gratuit !!!
Bonjooour 
Quelqu'un a une idée pour faire un angle de 60°... Sans rapporteur ? Mis à part le pif !
Papier quadrillé, j'y ai réfléchit, pas moyen de trouver.
( J'ai un exercice à faire... J'ai besoin d'un rapporteur, et je l'ai laissé sur place -_- )
Quelqu'un a une idée pour faire un angle de 60°... Sans rapporteur ? Mis à part le pif !
Papier quadrillé, j'y ai réfléchit, pas moyen de trouver.
( J'ai un exercice à faire... J'ai besoin d'un rapporteur, et je l'ai laissé sur place -_- )

- Saer Myenn
- Membre
- Messages : 4020
- Enregistré le : mer. 27 janv. 2010, 21:43
- Localisation : Tout est bon chez le héron
Re: Soutien Scolaire Gratuit !!!
On va faire comme ça... Merci  !
!
Hum seconde question... Dans ma rafale d'exercices, le dernier est le plus court... Pourtant, le sujet traité remonte au début de l'année, fin d'année de seconde.
Ultime trou de mémoire.

Voir l'image en grand
Le problème se pose aux deux dernières questions...
Je me souviens vaguement ce qu'est un ensemble de définition... Mais... Problème.
Je sais que c'est ou une droite, ou un cercle, qui englobe toutes les possibilités, sauf erreur de ma part.
Comment définir cet ensemble sur la figure ? :/
Le truc rapporte pas énormément de points sur la note finale, mais ça me tracasse, et j'arrive pas à répondre.
Hum seconde question... Dans ma rafale d'exercices, le dernier est le plus court... Pourtant, le sujet traité remonte au début de l'année, fin d'année de seconde.
Ultime trou de mémoire.

Voir l'image en grand
Le problème se pose aux deux dernières questions...
Je me souviens vaguement ce qu'est un ensemble de définition... Mais... Problème.
Je sais que c'est ou une droite, ou un cercle, qui englobe toutes les possibilités, sauf erreur de ma part.
Comment définir cet ensemble sur la figure ? :/
Le truc rapporte pas énormément de points sur la note finale, mais ça me tracasse, et j'arrive pas à répondre.

- Silver_lugia
- Membre
- Messages : 2741
- Enregistré le : ven. 04 avr. 2008, 20:52
- Localisation : 404 : membre non trouvée
Re: Soutien Scolaire Gratuit !!!
Hey ici ! Dites, j'ai un contrôle de maths demain sur les fonctions, chapitre que j'ai assez bien compris sauf un point : l'interpolation linéaire. Y a pas une âme matheuse et charitable pour me l'expliquer, siouplait ? *yeux du Chat Potté*

- Saer Myenn
- Membre
- Messages : 4020
- Enregistré le : mer. 27 janv. 2010, 21:43
- Localisation : Tout est bon chez le héron
Re: Soutien Scolaire Gratuit !!!
Tu prends deux points d'un repère A (0;6) et B (5;3,5). Tu calcules d'abord l'accroissement moyen pour une unité. (Formule : 'Yb-Ya/Xb-Xa' pour rappel).
Ensuite, tu prends l'ordonnée de A (6) à laquelle tu ajoutes une abscisse aléatoire, par exemple, 3 (pas trop grand quand même) multiplié au nombre trouvé auparavant.
Exemple : 6 (Ordonnée de A) + 3 (Nombre d'unité aléatoire) * (-0,5) = 6 - 1,5 = 4,5.
T'as compris ou non ?
Ensuite, tu prends l'ordonnée de A (6) à laquelle tu ajoutes une abscisse aléatoire, par exemple, 3 (pas trop grand quand même) multiplié au nombre trouvé auparavant.
Exemple : 6 (Ordonnée de A) + 3 (Nombre d'unité aléatoire) * (-0,5) = 6 - 1,5 = 4,5.
T'as compris ou non ?

- Silver_lugia
- Membre
- Messages : 2741
- Enregistré le : ven. 04 avr. 2008, 20:52
- Localisation : 404 : membre non trouvée
Re: Soutien Scolaire Gratuit !!!
Là tu es à la fois dans le plan et l'espace, ce qui n'a aucun sens.Saz Pan Rudo a écrit :Tu prends deux points d'un repère A (0;6) et B (5;3,5).
Re: Soutien Scolaire Gratuit !!!
3,5 ou encore 7/2, si tu préfères, Lamelune... 
Re: Soutien Scolaire Gratuit !!!
Bien le coucou, c'est encore moi, et mon traditionnel devoir de la semaine. ( Et encore, j'ai une vingtaine d'exos en plus à chaque fois dans la semaine. Bref. )
C'est donc des maths, de Première S.
Il ne reste qu'une question ._. !

La survivante est celle en rouge...
Comment faire pour trouver ça ? Je n'arrive pas à m'en dépatouiller, c'est l'unique question qui me bloque sur la fiche.
Merci d'avance à celui/celle qui aura une illumination pour me dépanner
C'est donc des maths, de Première S.
Il ne reste qu'une question ._. !

La survivante est celle en rouge...
Comment faire pour trouver ça ? Je n'arrive pas à m'en dépatouiller, c'est l'unique question qui me bloque sur la fiche.
Merci d'avance à celui/celle qui aura une illumination pour me dépanner

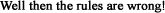
Re: Soutien Scolaire Gratuit !!!
Tu mets tout au même dénominateur, tu développes puis tu faits une identification des coefficients, car 2 polynômes sont égaux si et seulement si leurs coefficients sont égaux.
Donc tu développes (x+2)(ax+b) +c / x+2
= ax²+bx+2ax+2b+c / x+2
Or ton polynôme de départ est -x²-3x-3.
Donc a = -1
b+2a = -3
2b+c = -3
Faits la suite
Pour l'asymptote, quelle est la limite en l'infini de f(x) - ax+b ? Tu as du écrire un théorème là-dessus.
Donc tu développes (x+2)(ax+b) +c / x+2
= ax²+bx+2ax+2b+c / x+2
Or ton polynôme de départ est -x²-3x-3.
Donc a = -1
b+2a = -3
2b+c = -3
Faits la suite
Pour l'asymptote, quelle est la limite en l'infini de f(x) - ax+b ? Tu as du écrire un théorème là-dessus.
- Tyriak
- Membre
- Messages : 7071
- Enregistré le : jeu. 06 mai 2010, 18:51
- Localisation : ça dépend y a du café ?
Re: Soutien Scolaire Gratuit !!!
Et n'oublie pas de mentionner l'intervalle de départ dans tes démonstrations 
- /Salamence/
- Membre
- Messages : 306
- Enregistré le : mar. 08 déc. 2009, 13:51
Re: Soutien Scolaire Gratuit !!!
Si quelqu'un veut s'amuser à calculer la dérivée seconde de : racine de --> x-1 divisé par x+1 (tout est dans la racine quoi), ça m'aiderait bien xD. Parce que la résultat que j'obtiens dit que la fonction est concave sur (donc dérivée seconde négative) sur un intervalle ( ]-infinie; à environ -6,46).J'veux déjà avoir fait cette étude de fonction avant que le prof le fasse ...
Préalablement inscrit en tant que "Salamence Heart", mais compte piraté
Re: Soutien Scolaire Gratuit !!!
Bonjour à tous, j'ai une rédaction d'anglais à faire pour les vacances et j'aimerais savoir comment on dit en anglais :
"La gourmandise est un vilain défaut"
Merci
Edit : C'est bon, j'ai trouvé xD
"La gourmandise est un vilain défaut"
Merci
Edit : C'est bon, j'ai trouvé xD
Code Ami : 4313 - 2479 - 7433
Nom : Maxou
Type Safari : Combat
Pokémon : Pandespiègle, Machopeur & Hariyama
MP moi si vous voulez m'ajouter, merci!
Nom : Maxou
Type Safari : Combat
Pokémon : Pandespiègle, Machopeur & Hariyama
MP moi si vous voulez m'ajouter, merci!
- Pooh
- Membre
- Messages : 3476
- Enregistré le : sam. 01 août 2009, 22:11
- Localisation : Au pays du geek.
Re: Soutien Scolaire Gratuit !!!
Histoire de pas rester rouillé en maths, je l'ai fait/Salamence/ a écrit :Si quelqu'un veut s'amuser à calculer la dérivée seconde de : racine de --> x-1 divisé par x+1 (tout est dans la racine quoi), ça m'aiderait bien xD. Parce que la résultat que j'obtiens dit que la fonction est concave sur (donc dérivée seconde négative) sur un intervalle ( ]-infinie; à environ -6,46).J'veux déjà avoir fait cette étude de fonction avant que le prof le fasse ...
Partons du point de départ :
- Fonction étudiée : racine de => (x-1)/(x+1)
- Définie sur [1;+infini]
1e dérivée : On a un truc du genre (a/b)/c avec :
a = 1
b = racine carrée de => x²-1
c = x+1
2e dérivée : Idem, c'est de la forme (a/b)/c avec :
a = -2x +1
b = (x-1) (racine carrée de x²-1)
c = (x+1)²
Ya plus qu'à faire l'étude de signes..
a est négatif lorsque x > 0.5, positif lorsque x<0.5
x-1 négatif lorsque x < 1, positif lorsque x>1
La racine carrée n'existe que dans les intervalles ]-inf;-1] et [1;+inf[
Donc b est négatif en ]-inf;-1] et positif en [1:+inf[
c est toujours positif.
Conséquence : la dérivée seconde est toujours négative sur ]-inf;-1] et [1;+inf[
Faut juste que t'arrives à utiliser les dérivées de base et la factorisation pour arriver à ce résultat. Et être bien organisé.
- /Salamence/
- Membre
- Messages : 306
- Enregistré le : mar. 08 déc. 2009, 13:51
Re: Soutien Scolaire Gratuit !!!
En fait j'avais dérivé une racine à un moment, puis ce qu'i y avait dedans mais j'ai oublié de multiplier par 2x donc ça foirait tout  . Sinon effectivement c'était ça, merci quand même
. Sinon effectivement c'était ça, merci quand même  .
.
Préalablement inscrit en tant que "Salamence Heart", mais compte piraté
- Automne
- Membre
- Messages : 94
- Enregistré le : mer. 09 févr. 2011, 20:22
- Localisation : Alaska, chasse le caribou
Re: Soutien Scolaire Gratuit !!!
Quelqu'un saurait 4 façons d'ouvrir les propriétés d'un fichier?
j'en ai trouvé trois :
mais j'ai absolument pas d'idée pour la quatrième....
j'en ai trouvé trois :
Spoiler :
Re: Soutien Scolaire Gratuit !!!
Il suffit de faire ALT+Double Clic, et cela fonctionneAutomne14 a écrit :Quelqu'un saurait 4 façons d'ouvrir les propriétés d'un fichier?
j'en ai trouvé trois :mais j'ai absolument pas d'idée pour la quatrième....Spoiler :

