Soutien Scolaire Gratuit !!!
Re: Soutien Scolaire Gratuit !!!
Limite en quoi ? Un point fixe, -oo ou +oo ?
Re: Soutien Scolaire Gratuit !!!
On est en présence d'une forme indéterminé oo / oo: pour cela il faut que mettes en facteur le terme de plus haut degré ou appliquer la règle de l'hôpital:
http://limite.cours-de-math.eu/exercice ... ion-limite
Ce qui pourrait t'aider:
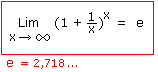
http://limite.cours-de-math.eu/exercice ... ion-limite
Ce qui pourrait t'aider:
Re: Soutien Scolaire Gratuit !!!
@Kuja
Après avoir compris que Lamelune te parle d'une fonction et est donc totalement HS,
(Sans parler de vouloir utiliser la règle de L'Hospital pour des suites, I lol'd.)
tu remarques que 2^(n+3) = 2^3 * 2^n = 8 * 2^n
Et donc Un = 8*(2/5)^n.
Comme 2/5 < 1, lim Un = 0.
EDIT: J'ai supposé que Un = (2^(n+3))/(5^n), et pas 2^((n+3)/5^n), hein, vu que t'as un parenthèsage ambigu. Si j'ai pris la mauvaise option, c't'un peu plus compliqué. Indice: Logarithme.
Après avoir compris que Lamelune te parle d'une fonction et est donc totalement HS,
(Sans parler de vouloir utiliser la règle de L'Hospital pour des suites, I lol'd.)
tu remarques que 2^(n+3) = 2^3 * 2^n = 8 * 2^n
Et donc Un = 8*(2/5)^n.
Comme 2/5 < 1, lim Un = 0.
EDIT: J'ai supposé que Un = (2^(n+3))/(5^n), et pas 2^((n+3)/5^n), hein, vu que t'as un parenthèsage ambigu. Si j'ai pris la mauvaise option, c't'un peu plus compliqué. Indice: Logarithme.
Hullabaloo a écrit :Ah Pod, mon amour.
Et je rappelle à tous mes fans qu'ils peuvent aller lire mes critiques cinéma parce que voilà.PalkiaPeårl a écrit :Vous ne battrez jamais Pod à son propre jeu. Si il dit que c'est pas ça/que ça a rien à voir/whatever, c'est qu'il a raison. Et vous ne pourrez rien y faire.
CA : 2492 - 4279 - 9345
(Si quelqu'un peut me dire quels pokés j'ai dans mon safari...)
(Si quelqu'un peut me dire quels pokés j'ai dans mon safari...)
Re: Soutien Scolaire Gratuit !!!
Pour ceux qui veulent le signe de l'infini : ∞
Re: Soutien Scolaire Gratuit !!!
Logarithme ? J'ai fait un ctrl+f mental, et ça me dit fichtrement rien.Pod607 a écrit :@Kuja
Après avoir compris que Lamelune te parle d'une fonction et est donc totalement HS,
(Sans parler de vouloir utiliser la règle de L'Hospital pour des suites, I lol'd.)
tu remarques que 2^(n+3) = 2^3 * 2^n = 8 * 2^n
Et donc Un = 8*(2/5)^n.
Comme 2/5 < 1, lim Un = 0.
EDIT: J'ai supposé que Un = (2^(n+3))/(5^n), et pas 2^((n+3)/5^n), hein, vu que t'as un parenthèsage ambigu. Si j'ai pris la mauvaise option, c't'un peu plus compliqué. Indice: Logarithme.
Mais ta version me semble plus juste, merci

Re: Soutien Scolaire Gratuit !!!
Pas sûr: tu n'as jamais vu des notations du genre un = f(n) ou un+1 = f(un) pour étudier les variations d'une suite un peu compliquée ?Pod607 a écrit :@Kuja
Après avoir compris que Lamelune te parle d'une fonction et est donc totalement HS,
.
Je faisais ça pour des suites avec des racines carrés.
Re: Soutien Scolaire Gratuit !!!
Si.Lamelune a écrit :Pas sûr: tu n'as jamais vu des notations du genre un = f(n) ou un+1 = f(un) pour étudier les variations d'une suite un peu compliquée ?Pod607 a écrit :@Kuja
Après avoir compris que Lamelune te parle d'une fonction et est donc totalement HS,
.
Je faisais ça pour des suites avec des racines carrés.
Question subsidiaire : Penses-tu que ce soit pertinent ici?
Hullabaloo a écrit :Ah Pod, mon amour.
Et je rappelle à tous mes fans qu'ils peuvent aller lire mes critiques cinéma parce que voilà.PalkiaPeårl a écrit :Vous ne battrez jamais Pod à son propre jeu. Si il dit que c'est pas ça/que ça a rien à voir/whatever, c'est qu'il a raison. Et vous ne pourrez rien y faire.
CA : 2492 - 4279 - 9345
(Si quelqu'un peut me dire quels pokés j'ai dans mon safari...)
(Si quelqu'un peut me dire quels pokés j'ai dans mon safari...)
Re: Soutien Scolaire Gratuit !!!
Peut être pas, j'avais pas remarqué que c'étais de la forme a^m+n
- Voltali Fessenheim
- Légende Pokébipienne
- Messages : 11406
- Enregistré le : mer. 26 août 2009, 14:17
Re: Soutien Scolaire Gratuit !!!
Le ln descend les puissances, ca a pas que la seule utilité de briser exp
D'ailleurs c'est plus souvent utilisé dans ce genre de transformation croissante pour s'amuser à trouver des choses chiantes :/
D'ailleurs c'est plus souvent utilisé dans ce genre de transformation croissante pour s'amuser à trouver des choses chiantes :/
Re: Soutien Scolaire Gratuit !!!
Un indice à Kuja: a^x = x ln(a) et ln(ab) = ln(a)+ln(b)
Re: Soutien Scolaire Gratuit !!!
Ah oui, compris. Je me disais que ça allait pas.
J'ai proposé mes résultats à trois autres personnes, on a tous pareil... J'en conclus que c'est bon.
Merci, et vivent les maths !
J'ai proposé mes résultats à trois autres personnes, on a tous pareil... J'en conclus que c'est bon.
Merci, et vivent les maths !

-
-----------
- Membre
- Messages : 596
- Enregistré le : mar. 10 juil. 2007, 14:46
Re: Soutien Scolaire Gratuit !!!
Bonjourbonjour
Je dois déterminer pour lundi la limite en 0 de 1-cosx / x , sachant que cosx = 1 je suis face à une F.I. et donc bloqué ... Si quelqu'un pouvais me donner des pistes
et donc bloqué ... Si quelqu'un pouvais me donner des pistes  ( j'ai comme aide : penser à l'approximation affine de la fonction cosinus mais ça m'aide pas des masses >>' )
( j'ai comme aide : penser à l'approximation affine de la fonction cosinus mais ça m'aide pas des masses >>' )
Merci d'avance '
'
Je dois déterminer pour lundi la limite en 0 de 1-cosx / x , sachant que cosx = 1 je suis face à une F.I.
Merci d'avance
Re: Soutien Scolaire Gratuit !!!
lim (x-->0) [1 - cos(x)]/x
= lim (x-->0) {[1 + cos(x)] * [1 - cos(x)]}/{x * [1 + cos(x)]}
= lim (x-->0) [1 - cos²(x)]/{x * [1 + cos(x)]}
= lim (x-->0) sin²(x)/{x * [1 + cos(x)]}, since 1 - cos²(x) = sin²(x)
= lim (x-->0) {sin(x) * sin(x)/x * 1/[1 + cos(x)]}
= lim (x-->0) sin(x) * lim (x-->0) sin(x)/x * lim (x-->0) 1/[1 + cos(x)]
= 0 * 1 * 1/2
= 0.
= lim (x-->0) {[1 + cos(x)] * [1 - cos(x)]}/{x * [1 + cos(x)]}
= lim (x-->0) [1 - cos²(x)]/{x * [1 + cos(x)]}
= lim (x-->0) sin²(x)/{x * [1 + cos(x)]}, since 1 - cos²(x) = sin²(x)
= lim (x-->0) {sin(x) * sin(x)/x * 1/[1 + cos(x)]}
= lim (x-->0) sin(x) * lim (x-->0) sin(x)/x * lim (x-->0) 1/[1 + cos(x)]
= 0 * 1 * 1/2
= 0.
-
-----------
- Membre
- Messages : 596
- Enregistré le : mar. 10 juil. 2007, 14:46
Re: Soutien Scolaire Gratuit !!!
Merci Lamelune *o*
Tu utilises la quantité conjuguée , c'est ça ?
Je te suis pas jusqu'à la fin (niveau 1ère S XD ) ça veut dire quoi since ? ( tu m'a paumé à la 4ème ligne )
(niveau 1ère S XD ) ça veut dire quoi since ? ( tu m'a paumé à la 4ème ligne )
Tu utilises la quantité conjuguée , c'est ça ?
Je te suis pas jusqu'à la fin
Re: Soutien Scolaire Gratuit !!!
J'ai un peu fait compliqué mais je te donne une piste plus simple:
1-cos(x) /x = 1/x - cos(x)/x
1-cos(x) /x = 1/x - cos(x)/x
-
-----------
- Membre
- Messages : 596
- Enregistré le : mar. 10 juil. 2007, 14:46
Re: Soutien Scolaire Gratuit !!!
Mais avec ta piste , je suis obligé de séparer 0+ et 0- et par somme je trouve + l'infini en 0+ et F.I. En 0-  ( sauf erreur de calcul >>')
( sauf erreur de calcul >>')
Re: Soutien Scolaire Gratuit !!!
Ca ne marche pas car on tombe sur une FI oo - oo
Et pour le since, il fait référence à une formule donc qui n'a rien à voir avec le calcul
Et pour le since, il fait référence à une formule donc qui n'a rien à voir avec le calcul
-
-----------
- Membre
- Messages : 596
- Enregistré le : mar. 10 juil. 2007, 14:46
Re: Soutien Scolaire Gratuit !!!
Formule que je ne pense pas avoir vu ....Lamelune a écrit :Ca ne marche pas car on tombe sur une FI oo - oo
Et pour le since, il fait référence à une formule donc qui n'a rien à voir avec le calcul
Merci pour ton aide en tout cas
Je continuerai à chercher demain ( j'aurai 20 à ce fichu DM XD c'est un défi
-
MisterPrince
- Membre
- Messages : 9
- Enregistré le : mar. 29 mars 2011, 18:17
Re: Soutien Scolaire Gratuit !!!
Bonjour ! C'est juste pour dire que étant en license 2 de maths, je peux aider en maths et physique (bien qu'apparament, il y en ai un paquet qui puisse aider en maths ici)
Je confirme la solution en 0+ et 0-, la limite c'est 0 (mais bon, j'utilise un dévellopement limité qu'on voit pas avant l'université ...)
Je confirme la solution en 0+ et 0-, la limite c'est 0 (mais bon, j'utilise un dévellopement limité qu'on voit pas avant l'université ...)
